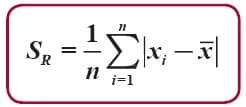Pada kesempatan kali ini pengaja.co.id akan membuat artikel yang berjudul Rumus Simpangan Rata Rata yang mana akan membahas mengenai : Pengertian, Contoh Soal & Cara Menghitungnya
Pengertian Rumus Simpangan Rata Rata
Pengertian simpangan rata-rata atau (mean deviasi) adalah jarak antara nilai data dan menuju rata-rata.
RS termasuk dalam ukuran penyebaran data, serta dalam varian dan standar deviasi. Tujuannya adalah untuk mengetahui berapa nilai data yang menyimpang dari rata-rata sebenarnya.
Rumus Simpang Rata-Rata
Sekumpulan data kuantitatif yang tidak berkelompok dan dinyatakan dengan X1, X2, …, Xn. dari data tersebut bisa kita tentukan simpangan rata-rata (SR) dengan menggunakan rumus seperti dibawah ini :
Contoh Soal 1 :
Hitunglah simpangan rata-rata dari nilai ulangan Matematika siswa Kelas XI SMK PGRI 2 Tanjung Raja seperti yang ada pada Tabel 1 berikut ini :
Tabel 1 Nilau ulangan matematika siswa Kelas XI SMK PGRI Tanjung Raja
| Interval Kelas | Frekuensi |
| 40-44 | 3 |
| 40-44 | 4 |
| 45-49 | 6 |
| 50-54 | 8 |
| 55-59 | 10 |
| 60-64 | 11 |
| 65-69 | 15 |
| 75-79 | 6 |
| 80-84 | 4 |
| 85-89 | 2 |
| 90-94 | 2 |
Penyelesaian :
Dari table diatas, dapat diperoleh hasil yang sudah dibulatkan yaitu 65,7
| Kelas Interval | Nilai Tengah (Xi | fi | Ix-xI | fi Ix-xI |
| 40-44 | 42 | 3 | 23,7 | 71,1 |
| 45-49 | 47 | 4 | 18,7 | 74,8 |
| 50-54 | 52 | 6 | 13,7 | 82,2 |
| 55-59 | 57 | 8 | 8,7 | 69,6 |
| 60-64 | 62 | 10 | 3,7 | 37 |
| 65-69 | 67 | 11 | 1,3 | 14,3 |
| 70-74 | 72 | 15 | 6,3 | 94,5 |
| 75-79 | 77 | 6 | 11,3 | 67,8 |
| 80-84 | 82 | 4 | 16,3 | 65,2 |
| 85-89 | 87 | 2 | 21,3 | 42,6 |
| 90-94 | 92 | 2 | 26,3 | 52,6 |
| Σfi = 71 | Σfi |x – x| = 671,7 | |||
Maka, simpangan rata-rata (SR) = 671,7 / 71 = 9,46
Peringatan :
Simpangan rataan hitung seperti diatas menunjukan rataan hitung jauhnya datum dari rataan hitung.
Cara menghitung simpangan baku dari data kuantitatif : 2, 5, 7, 4, 3, 11, 3 menggunakan kalkulator ilmiah (fx-3600Pv) adalah seperti dibawah ini :
| 1) | Kalkulator “ON” |
| 2) | MODE 3 Program SD |
| 3) | Masukan data |
| 2 data | |
| 5 data | |
| … | |
| … | |
| … | |
| 3 data | |
| 4) | Tekan tombol X an-1 |
| a = 2,878491669 = 2,88 | |
Contoh Soal 2 :
Hitunglah simpangan rata-rata dari data keuantitatif seperti dibawah ini :
12, 3, 11, 3, 4, 7, 5, 11
Pembahasan
Maka, simpangan rata-rata adalah 3,25
Kalian bisa mencoba menentukan simpangan rata-rata seperti diatas dengan menggunakan kalkulator. Lihat hasilya sama atau tidak?
Untuk sekumpulan data yang dinyatakan oleh X1, X2, …Xn dan nilai masing-masing dari data tersebut mempunyai frekuensi f1, f2, …, fn maka akan didapatkan nilai simpangan rata-rata (SR)dengan menggunakan rumus :
-
Simpangan Rata-Rata Dengan Data Tunggal
Rumus Variasi (S2) dari Data Tunggal
Rumus variasi dari data tunggal seperti yang akan dijelaskan dibawah ini :
Keterangan:
xi= nilai data ke-i
x= rata-rata
n = jumlah seluruh frekuensi
Rumus Standar Deviasi/Simpangan Bakunya Data Tunggal yaitu :
rumus simpangan baku data tunggal dapat dinyatakan melalui persamaan seperti dibawah ini :
Keterangan:
xi = nilai data ke –i
x = rata-rata
n = jumlah seluruh frekuensi
-
Simpangan Rata-Rata Data Berkelok
Rumus Simpangan rat-rata (SR) data Berkelompok yaitu seperti dibawah ini :
Keterangan:
n = jumlah seluruh frekuensi
fi = frekuensi kelas ke-i
xi = nilai tengah kelas ke-i
x = rata-rata
k = banyaknya kelas interval
Variasi (Ragam)
Persamaan untuk variasi (ragam) seperti rumus dibawah ini :
Keterangan:
xi = nilai tengah kelas ke-i
fi = frekuensi kelas ke-i
x = rata-rata
k = banyak kelas interval
Starndar Deviasi atau Simpangan Baku
Rumus Simpangan baku untuk data kelompok yaitu seperti dibawah ini :
Keterangan:
xi = nilai tengah kelas ke-i
fi = frekuensi kelas ke-i
x = rata-rata
k = banyak kelas interval
Demikianlah artikel dari pengajar.co.id yang berjudul Rumus Simpangan Rata Rata : Contoh Soal & Cara Menghitungnya, semoga dengan adanya artikel ini bisa bermanfaat dan lebih menambah wawasan anda.